edongashi Shënimet e ushtrimeve
Aritmetika e numrave me pikë të lëvizshme
Nëse përdorim 32 bita përmes 2-komplementit, kemi mundësi t’i paraqesim $2^{32}$ kombinime në intervalin $-2^{31} \dots 2^{31}-1$.
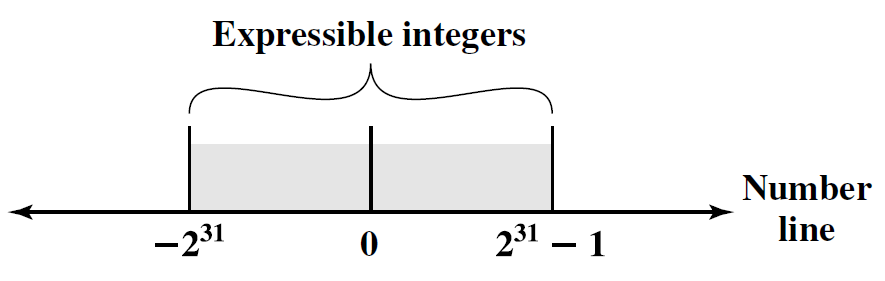
Nëse përdorim IEEE 754 formatin për të përafruar numra real, kemi mundësi të paraqesim intervalet:
- Numrat negativ: $-(2-2^{-23})\times 2^{128}\;\dots\; {-2}^{-127}$
- Numrat pozitiv: $2^{-127} \;\dots\; (2 - 2^{-23}) \times 2^{128}$
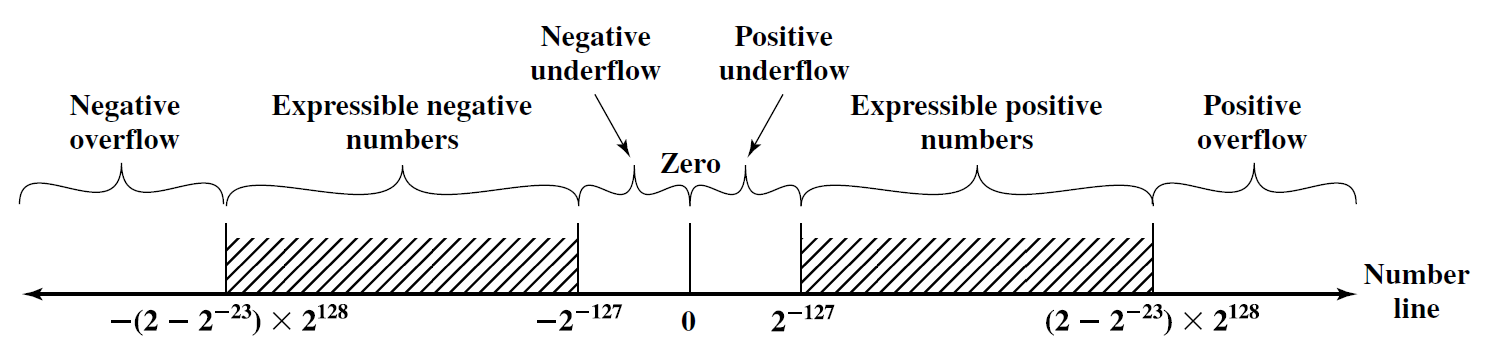
5 regjione mbesin të pa paraqitura:
- Numrat negativ më të vegjël se $-(2-2^{-23})\times 2^{128}$ - overflow negativ.
- Numrat negativ më të mëdhenj se ${-2}^{-127}$ - underflow negativ.
- Zeroja.
- Numrat pozitiv më të vegjël se $2^{-127}$ - underflow pozitiv.
- Numrat pozitiv më të mëdhenj se $(2 - 2^{-23}) \times 2^{128}$ - oferflow pozitiv.
Problemet:
- Formati i diskutuar deri më tash nuk ka mundësi ta paraqesë zeron.
- Overflow ndodh kur rezultati ka vlerë absolute shumë të madhe.
- Underflow ndodh kur rezultati ka vlerë absolute shumë të vogël.
Underflow mund të përafrohet me zero prandaj nuk paraqet aq humbje sa overflowi.
Numrat e paraqitur me pikë të lëvizshme nuk kanë shpërndarje uniforme.
Vlerat e mundshme janë më të shpeshta më afër origjinës ndërsa rrallohen në amplituda të mëdhaja.

Shumë operacione me numra të mëdhenj duhet të rrumbullakësohen.
Dy karakteristika:
- Shtrirja - nëse zmadhojmë bitat e eksponentit kemi më shumë gjerësi.
- Preciziteti - nëse zmadhojmë bitat e fraksionit kemi më shumë saktësi.
Për një madhësi fikse bitash, zmadhimi i precizitetin e ulë shtrirjen dhe e kundërta.
Standardi IEEE 754 definon numrat me pikë të lëvizshme në dy madhësi:
- 32-bitëshe - single precision (8 eksponenti, 23 fraksioni).
- 64-bitëshe - double precision (11 bit eksponenti, 52 bit fraksioni).
Përveç formatit 32 dhe 64 bitësh, standardi IEEE 754 definon dy formate të zgjeruara.
Këto formate përdoren për operacione të ndërmjetshme matematikore për ta minimizuar humbjen e saktësisë si shkak i rrumbullakësimeve.
Parametrat e IEEE 754 numrave
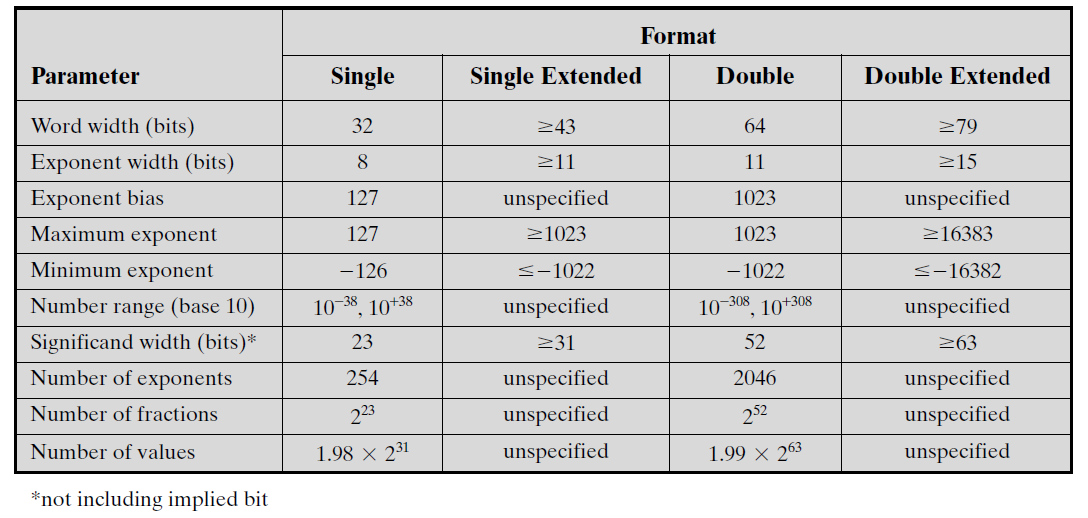
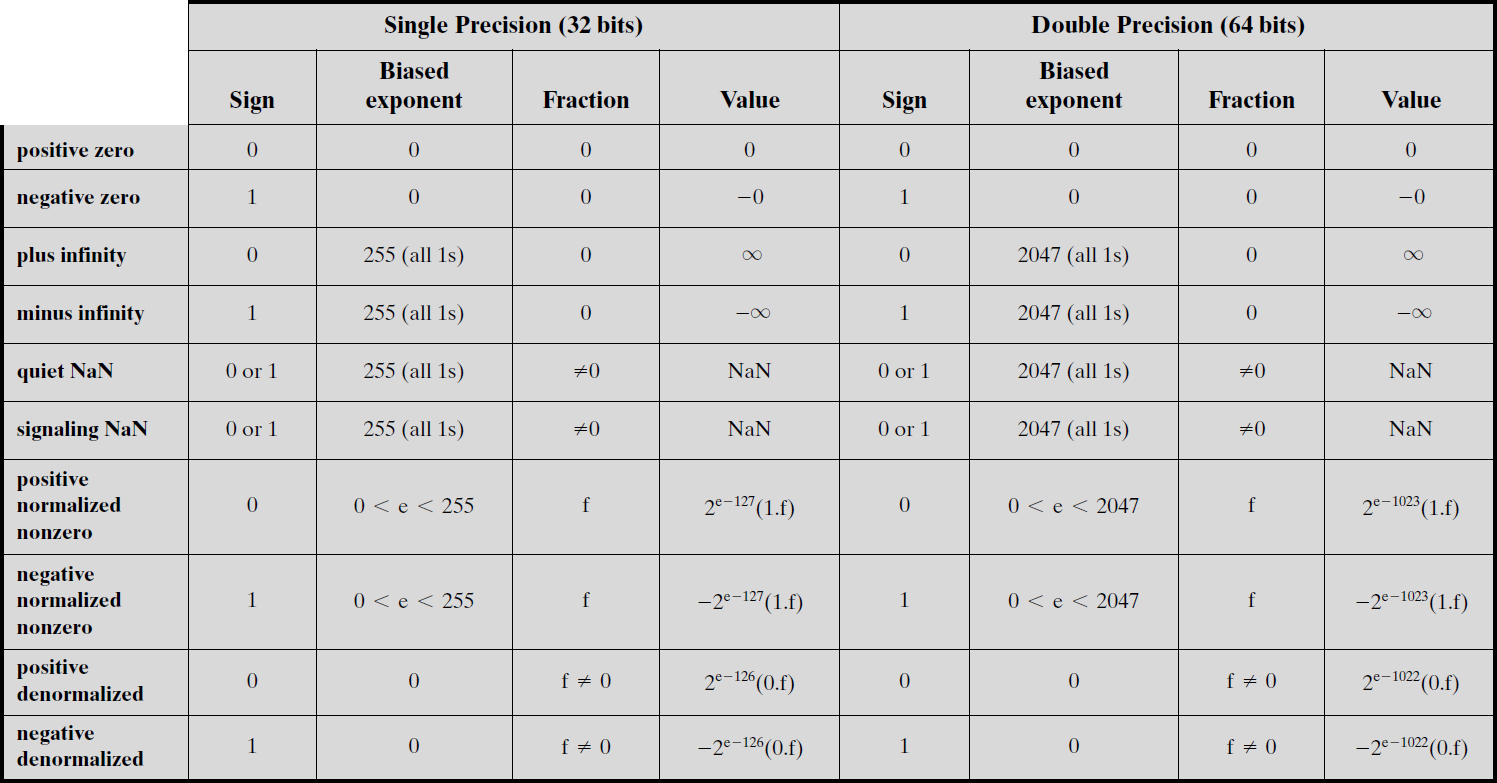
Paraqitja e numrave të normalizuar
Vlerat e eksponentit $1\dots 254$ për single dhe $1\dots 2046$ për double përdoren për ta paraqitur numrin e normalizuar të ndryshëm nga zero.
Paraqitja e zeros
Eksponenti zero me fraksion zero paraqet vlerën zero pozitive ose negative, varësisht nga biti i shenjës.
Paraqitja e infinitit
Eksponenti me të gjitha bitat 1 dhe fraksionin zero paraqet vlerën e infinitit pozitiv ose negativ, varësisht nga biti i shenjës.
Paraqitja e numrave të denormalizuar
Eksponenti me të gjitha bitat 0 dhe fraksionin jo-zero paraqet numër të denormalizuar.
Numri i denormalizuar ka formën $0.bbb\dots$
Në këtë rast eksponenti efektiv është $-126$ ose $-1022$ dhe numri është pozitiv ose negativ varësisht nga biti i shenjës.
Paraqitja e NaN
Eksponenti me të gjitha bitat 1 dhe fraksionin jo-zero konsiderohet si vlera NaN - Not a Number.
NaN përdoret për të paraqitur ndonjë gabim të ndodhur gjatë operacioneve.
Aritmetika e numrave me pikë të lëvizshme
Mbledhja dhe zbritja
Te numrat me pikë të lëvizshme, procesi i mbledhjes/zbritjes është më kompleks se i shumëzimit/pjesëtimit.
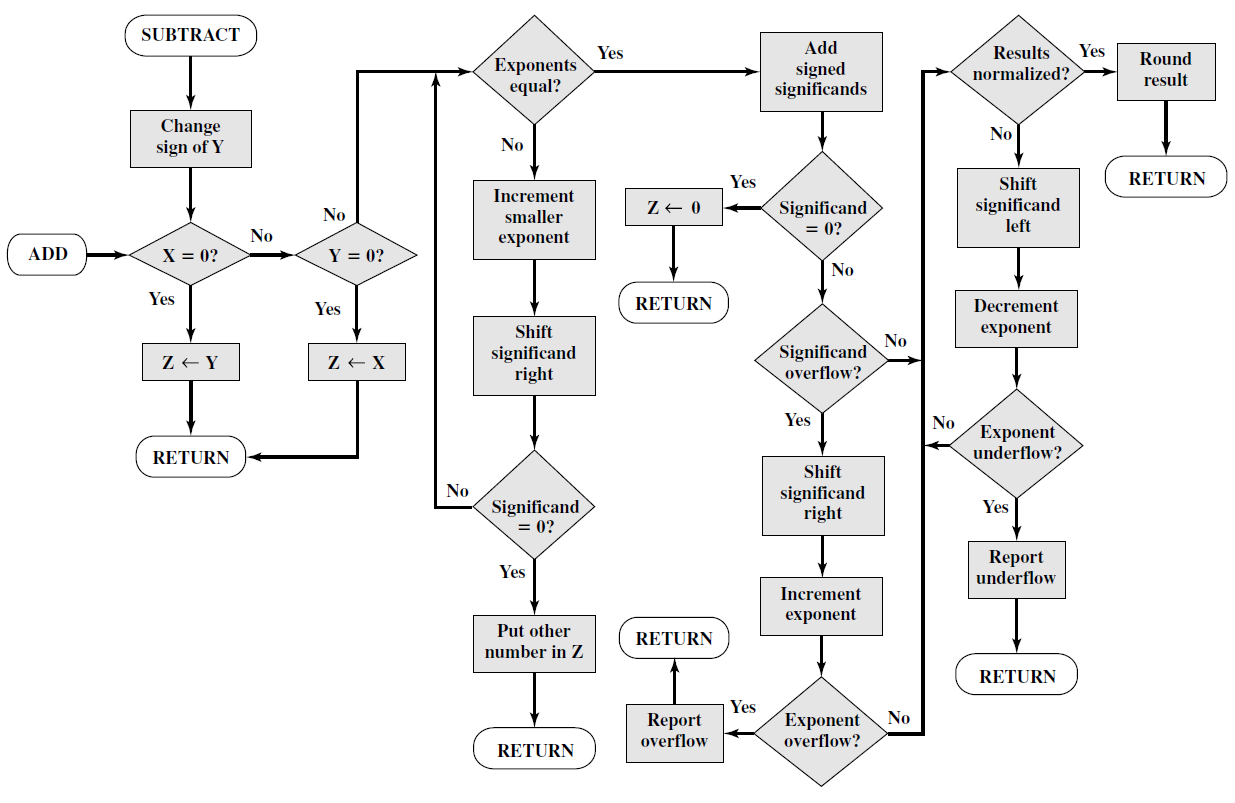
Algoritmi i mbledhjes/zbritjes:
- Kontrollo për zero.
- Përputhi fraksionet.
- Mbledhi ose zbriti fraksionet.
- Normalizo rezultatin.
Faza 1: Testimi për zero
Nëse kemi zbritje atëherë realizohet procesi i mbledhjes por me numrin i cili ka bitin e shenjës të kundërt.
Nëse ndonjëri operand është zero, rezultati është sa numri tjetër ($A + 0 = 0 + A = A$).
Faza 2: Përputhja e eksponentit
Për këtë fazë biti implicit i normalizimit duhet të bëhet eksplicit.
Numrat me eksponentë të ndryshem nuk mund të mbledhen/zbriten, prandaj duhet të përputhen eksponentët duke e zmadhuar eksponentin më të vogël.
Për çdo cikël shtyhet fraksioni djathtas dhe rritet eksponenti për 1 deri sa të barazohet me tjetrin.
Faza 3: Mbledhja
Fraksionet mbledhen duke marrë parasysh shenjat e tyre.
- Në rast se shuma del 0, rezultati del 0.
- Në rast se kemi overflow për 1 shifër, rritet eksponenti për 1 dhe shtyhet fraksioni djathtas për 1 pozitë.
Nëse kemi tejkalim të eksponentit konsiderohet si gabim dhe operacioni ndalohet.
Faza 4: Normalizimi
Rezultati normalizohet duke e shtyer fraksionin majtas deri sa të arrihet biti i parë jo-zero. Për çdo shtyerje zvogëlohet eksponenti për 1.
Përfundimisht rrumbullakësohet rezultati dhe kthehet.
Shumëzimi dhe pjesëtimi
Shumëzimi/pjesëtimi janë më të thjeshta se mbledhja/zbritja.
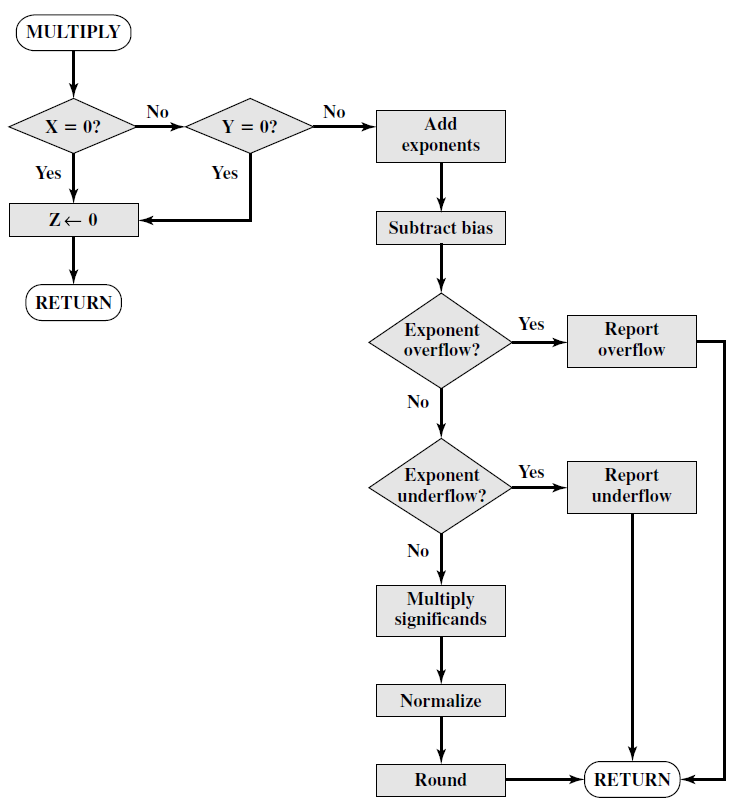
Shumëzimi
- Kontrollo për zero.
- Mbledhi eksponentët.
- Shumëzo fraksionet.
- Normalizo rezultatin.
Faza 1: Testimi për zero
Nëse ndonjëri operand gjatë shumëzimit është zero, atëherë i gjithë rezultati është zero.
Faza 2: Mbledhja e eksponentëve
Mbledhen eksponentët dhe i zbritet shtyerja (bias) për shkak të dyfishimit.
\[\overbrace{(X + B)}^{E_X} + \overbrace{(Y + B)}^{E_Y} - B = (X + Y) + B\]Nëse kemi tejkalim të intervalit valid atëherë kemi gabim.
Faza 3: Shumëzimi i fraksioneve
Shumëzohen fraksionet duke marrë parasysh shenjat e tyre.
Shumëzimi është sikur i numrave të plotë.
Faza 4: Normalizimi
Gjatë shumëzimit të fraksioneve rezultati del dyfish në gjatësi, me 2 shifra të pjesës së plotë.
Nëse biti më i madh del 1 atëherë shtyhet presja për 1 pozitë majtas duke e rritur eksponentin për 1.
Përfundimisht rrumbullakësohet rezultati në bitat e rezervuar për fraksionin dhe kthehet.
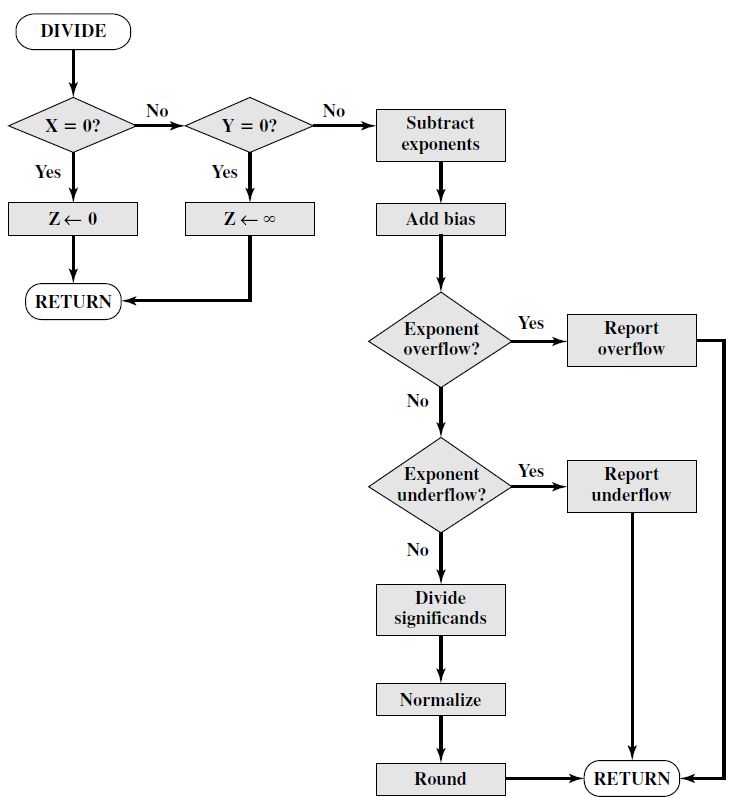
Pjesëtimi
- Kontrollo për zero.
- Zbrit eksponentët.
- Pjesëto fraksionet.
- Normalizo rezultatin.
Siç u cek, gjatë përputhjes së eksponentëve fraksionet duhet të shtyhen djathtas, me ç’rast ndodh humbja e bitave të vegjël.
Zakonisht ALU ka më shumë bita sesa që ruhen në fraksion. Këta bita shtohen si zero në të djathtë dhe quhen guard bita.
Guard bitat e zvogëlojnë humbjen gjatë procesit të shtyerjes dhe të shumëzimit.
Rrumbullakësimi
Gjatë operacioneve rezultati del me më shumë bita sesa operandët. Bitat shtesë duhet të mënjanohen duke i rrumbullakësuar.
Ekzistojnë 4 mënyra rrumbullakësimi:
- Rrumbullakëso te më i afërti numër i paraqitshëm.
- Rrumbullakëso në drejtim të $+\infty$.
- Rrumbullakëso në drejtim të $-\infty$.
- Rrumbullakëso në drejtim të zeros.
Standardi IEEE 754 për aritmetikën e numrave me pikë të lëvizshme i definon disa relacione në aspekt me rrumbullakësimin, infinitin, NaN, numrat e denomalizuar.
Infiniti
Çdo numër i fundëm $x$ i cili nuk është $\pm \infty$ e plotëson relacionin e krahasimit:
\[-\infty < x < +\infty\]Si dhe cilido operacion i mbledhjes/zbritjes së $x$ me vlerën $\pm\infty$ e jep $\pm\infty$.
Quiet NaN dhe Signaling NaN
- NaN sinjalizues paraqet një gabim gjatë veprimeve i cili lajmëron gabim.
- NaN i heshtur paraqet një gabim i cili vazhdon veprimet pa lajmëruar gabim.
NaN i heshtur ndodh kur kemi:
- Operacion mbi NaN sinjalizues.
- $(\pm\infty)+(\mp\infty)$ ose $(\pm\infty)-(\pm\infty)$
- $0\times\infty$
- $\frac{0}{0}$ ose $\frac{\infty}{\infty}$
- $x \;\%\; 0$ ose $\infty \;\%\; y$
- $\sqrt{x}, \quad x < 0$